How reasonable are you? Test your skills with these problems from new international Olympiad logic
In its only second year, the International Logic Olympiad has been booms as logic that is more important to our constant change in the world
Last month, 36 sharp high school students from the world’s footsteps and strong campus at Stanford University. With the exception of more than 4,000 students from more than 2,000 schools over 90 different countries, these 36 people are selected to compete like finalists in the second international Olympiad (orphan).
The competition includes three rounds of trials, which ended at the end of Stanford. There are teams of two to four shares in a war with wits, solve Logic puzzles and competes with Math Games Against the backdrop of foothills in Palo Alto, Calif. This year’s winners is the official moniker “Team Goblin Skin” in a Sky Skit “in a” Team Scit “Team” Tempuy GOBLIN SHOP “INSIDE IN THE ENGLISH ARO” KING-GUBGIN SI Luke “The key to their success, they argue, a lot of practice and team work.” I think about the reason I can do good to it because our friends are good, “we say.
Stanford computer scientist and oniciano launched Michael Genesereth in a collaboration between university and educational non-pharmacy-luminous. “We used the logic of almost everything we do,” Genesereth said. Doctors use the reasoning to know patients, lawyers use logical court arguments, and logic is more important than evaluating the world’s strong change around us, he says. “Not everyone has to do with math and formula and algebra,” more Genesereth.
In support of science journalism
If you enjoy this article, think about supporting our winning journalism in Subscribe. By purchasing a subscription you helped to ensure the future of influential stories about the discoveries and ideas that make our world today.
Most winners this year have a computer science, along with environmental science, is applied to mathematical engineering, but Zhang says that he “strong suit” and planned to go to political science. “Many problems require great thought and solutions to creation, and I think it helps me when I go to the future policy,” he explained.
A special aspect of the Olympiad is its identical attitude, where teams can work together to solve problems, Yin said. He was proud of how he and his teammates collaborated with a puzzle called countries (UNDER). After he argues that a solution offered by one of his or her group should be wrong and has an alternative that I speak well with his team, “Yin said it was a wonderful person to work with our group.”
Here are some curate puzzles from the competition you can try your hand with a friend group yourself. Some of the puzzles are edited to better fit the format of this article.
Friends
Four students, counted 1, 2, 3 and 4, voting themselves to know who should lead their review session. Every student is required to vote “yes” or “no” for each person in the group, including themselves. The following is the real statements about their ballots:

At the table above, statements from the original orphanage problem in the language of mathematical logic is correct. Our translations of the statements left.
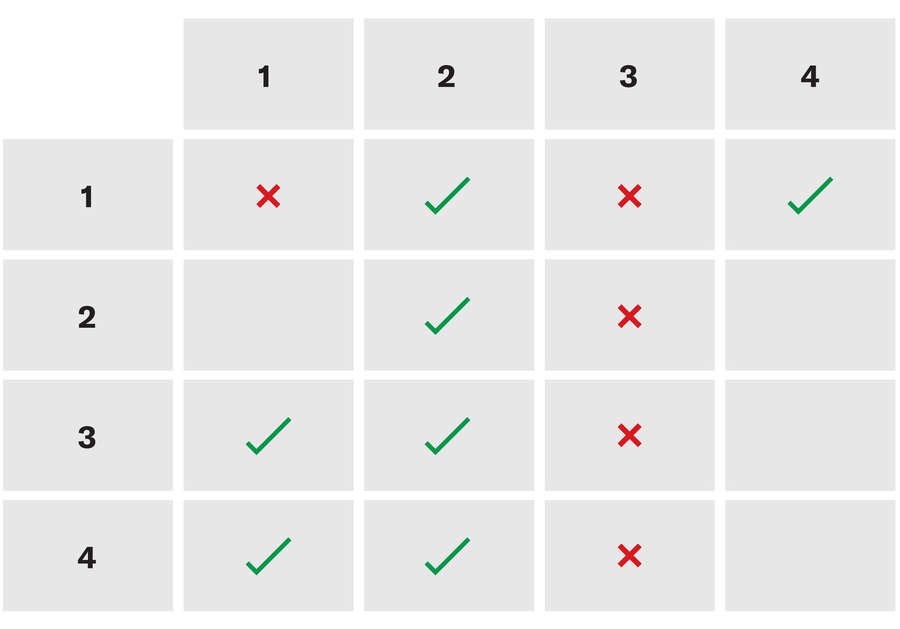
Find out, as possible from these statements, doing nothing and not to vote for whom. Fill in that of the following grids in a check for a yesot vote, an “x” for a vote and a blank if you don’t know that. Each row represents the ballot of the number listed on the left.
Note: If we have a statement art That is not true, we consider any sentence in the form “if A, THEN Chamanyhi“TRUE. For example,” If the sky is green, then ____ “true no matter what is in the blank. You need this fact to solve the puzzle.
QUIZ
1. What is the answer to question 2?
A. B
B. A
C. D
D. C
2. What is the answer to question 3?
A. C
B. D
C. B
D. A
3. What is the answer to question 4?
A. D
B. A
C. C
D. B
4. What is the answer to question 1?
A. D
B. C
C. A
D. B
CRACKING Safe
A secure safety opens in a series of four switches that can flip to (1) or off (0). Safe is broken, so can it open it, you need to get the position of two particular switches correctly – but no one knows which switches are important. Find the smallest set of combinations you can try to make sure that one of them will open safely.
nations
There are two types of countries: loud and weak. Only weak countries can invade, and the strong countries that can afford. If a strong country invades a weak country, it will grow in weak country, but it can be weak, and so strong, for some time period. Only a strong country can invade a weak country at a time. If many countries decide to invade the same weak country, one is selected to be allowed to invade. Each country wants to be as big as possible but not at the expense that has been annexed itself. Think of all countries perfectly reasonable. There are five strong countries and a weak country. Will weak country attack?
Hint: Try starting a strong country and a weak country first and then from there. To solve the problem, try how complex cases can be reduced by simple and nobreak;
Sudoku Puzzle
This puzzle also included in orphan. Competitors must resolve them under a time limit using only one pencil and paper.
Friends
QUIZ
1. D
2. C
3. B
4. A
CRACKING Safe
To make sure you can crack safety, you need to have every possible set of positions for each pair of switches represented. In that case, any two moves the things that matter or which positions are opened, one of the codes will crack it. The minimum number of combinations required is five. Here is a possible solution: 1000, 0100, 0010, 0001, 1111.
nations
Here’s a way of thinking about it. Suppose a strong country and a weak country. The strong country naturally wants to invade weak because no other country invades the strong after it. What about two strong countries and a weak country? Well, if one of the strong countries will claim the weak country, it can be temporarily weak and attack each other, so they do not want to invade the first return. Now consider three powerful countries and a weak country: again, when a strong country to invade, we have left a strong country and a situation we never invade this case. Using the same logic, if there are four strong countries, and the one who invades, the scenario will blame the three nations that are strong where everyone wants to invade, so no one in four countries invade the first place. In the end, this brings us to five powerful countries and a weak country, a scenario where all strong countries want to invade because, once a strong countries and one become weak.










