This problem with blocking-stacking math has a preposterous solution you need to see to believe
In principle, this impossible math allows for a bridle free glue to published blocks that can be across the Grand Canyon – and Infinity
Here’s an experimental blow in the mind you can try at home: gather in children’s blocks and put them on a table. Take a block and slowly push it along the table, inch by inch, until it’s in the fall of fall. If you have a patience and a steady hand, you need to balance it so that exactly half of it hangs on the edge. Make it anything more distant, and the gravity of victory. Now take two blocks and start. Hitting one on top of others, how far do you get the top of the top block to focus on the edge of the table?
Continue. Stacking multiple blocks as you can, what is the furthest overhang you can do before the total structural topples? Is it possible that the tower expands the full length of the block is beyond the lip on the table? Does physics allow both block lengths? The odd response is that the layered bridge can retreat forever. In principle, a freestanding stack of blocks can Days the Great CanyonNo glue required.
In support of science journalism
If you enjoy this article, think about supporting our winning journalism in Subscribe. By purchasing a subscription you helped to ensure the future of influential stories about the discoveries and ideas that make our world today.
Do not click “Checkout” in an infinite pack of Jenga blocks. Practical mundules like irregular forms of block, air waves and weight loss in an endless edifice can prevent your wishes in engineering. However, knowing why the overhang doesn’t have a limit to an ideal math world enlightened. Explanation prepares the harmonic series of mathematics and fitness concepts in the center of mass, two seemingly simple ideas with power. (For more fun, check: How tall do you build a tower without it to toppling?)
Your intuition can tell you that a block can be hanged in half its masses ahead of the table on the table before tipping. But why is that? Every thing has a center of mass-The is a point where we can find the full weight of the whole thing involved when we think about balance. As long as the mass center sits on top of the table, the object will remain placed. The moment the center of the mass passes into an edge, however, Weight pull the whole thing. In case of a spoon, something with irregular weight distribution, we can hang half of the utensil in a room before these tips, we have the same density (which is, they are uniformly density (that is, they do not have the same density (which is, they are uniformly density (which is, they are uniformly density (which is, they are uniformly density.
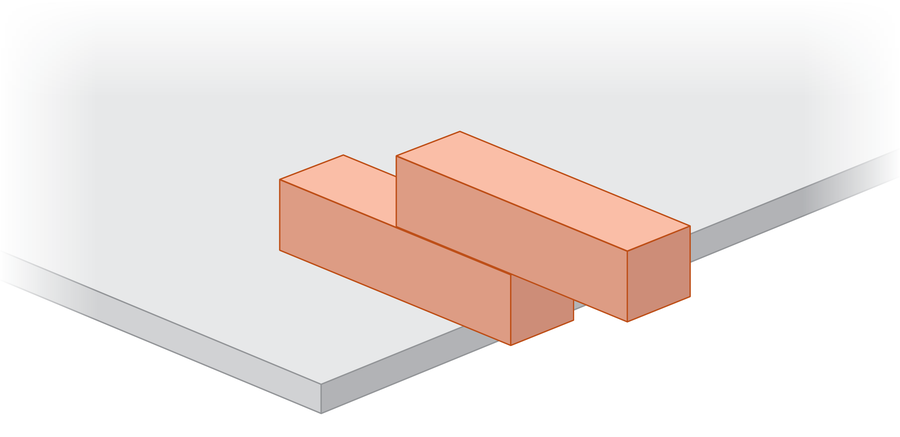
If we add more blocks, we need to give the center of the mass across the tower. Consider the case with two blocks. We know that the top block can expand half of its mass ahead of one of them. But after doing that, how far should we deny the bottom block?
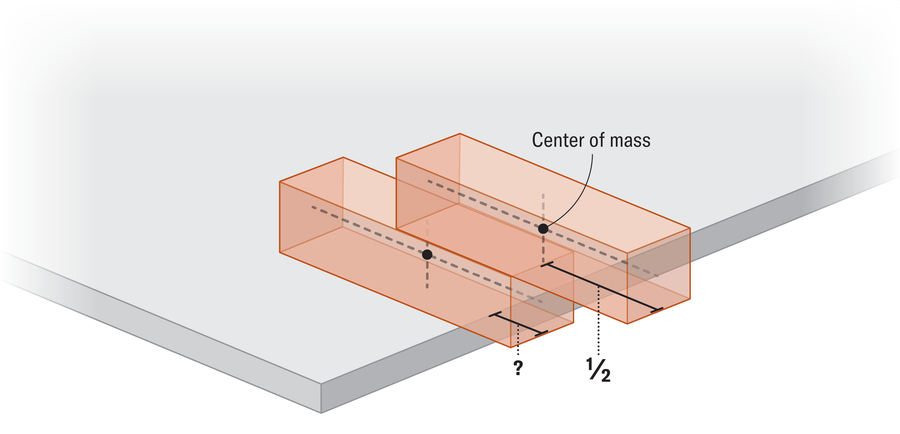
For simplicity, let’s say each block has a height of 1 and a mass of 1. You can see the bottom block can only be a quarter of the road (compare lengths in its entry). Sa kini nga punto, ang sentro sa masa sa taas nga bloke ug ang sentro sa masa sa ilawom sa blangko nga katumbas gikan sa sulab sa sulud sa sulud sa sulud sa sulud sa sulud sa kilid sa wala sa kilid Mao nga ang united center of mass of Two blocks of systems set up perfect balance above the edge of the table.
A pattern has emerged as we continue to add structural blocks. The top block extends 1/2 ahead of this one, the second block expands 1/4 beyond the block below it, the third expands 1/6The fourth enlarged 1/8then the next blocks float 1/10,, 1/12and so on. To find out why, let’s see another example. Suppose we have a strong tower with five blocks, and we want to add a sixth block below it and then slide the entire structure as possible. Conceptualization of this photo is helpful as two blocks: one with a mass of 5 on top of a block with an underground underground underground underground underground underground. We can then push the bottom block 1/12 to a unit ahead of the table on the table. How do we know that?
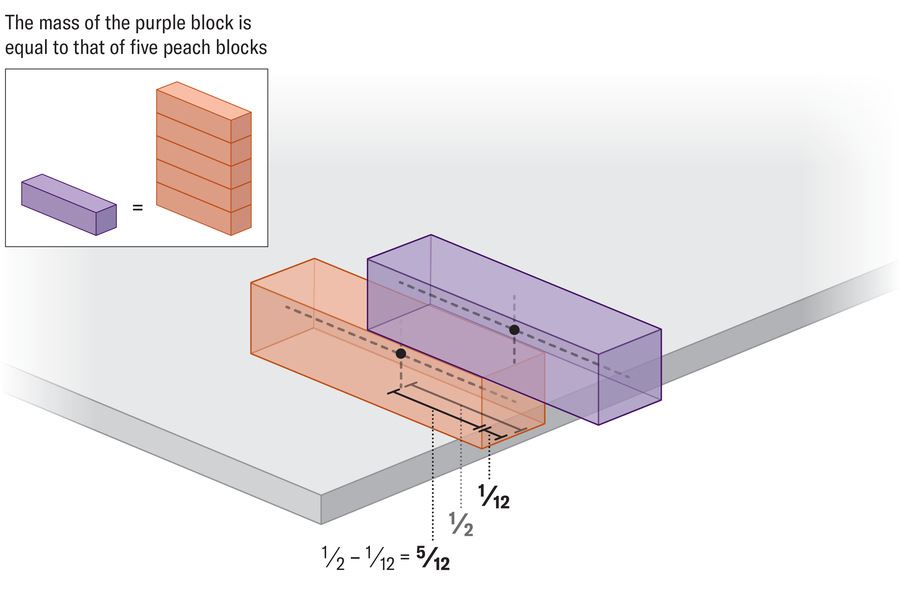
Once again, the answer has occurred to the mass centers of two blocks, at this time, because the underweight tabetop is higher than weight loss tabletop. It is known as lever-mind-minded how a book is heavier in the palm of your palms away from your body to be equal to a book that is tumbling in your torso. The distance between the center of the mass of the upper block and the edge of the table 1/12and the distance for the bottom block 1/2 – 1/12 = 5/12or five more times. Similar calculation reveals proper overhang at each tower level.
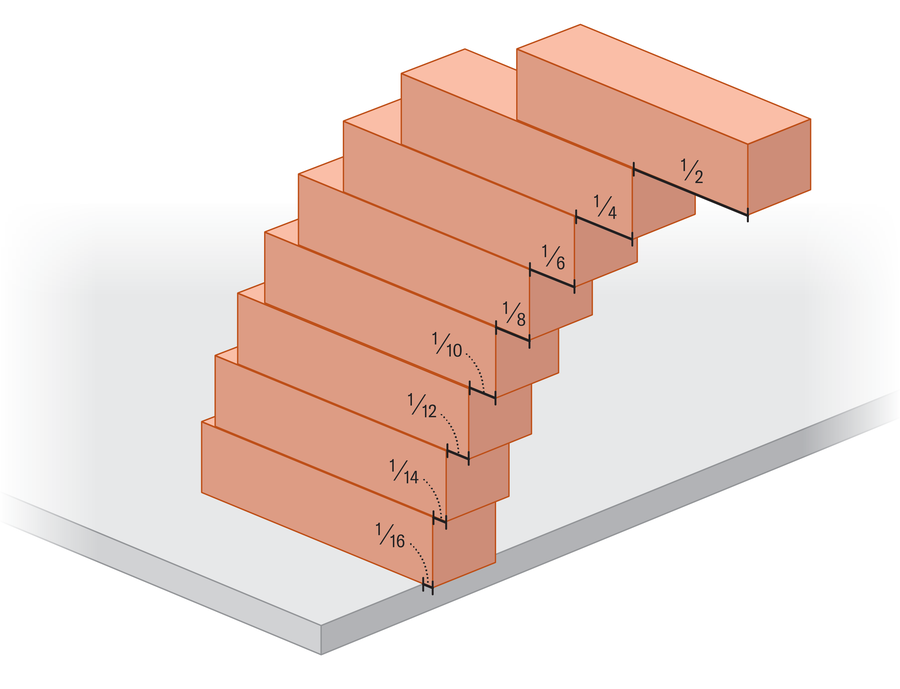
Answering our opening question (what is far from the tower given?) Worth adding all of these consecutive overhangs. If you have 10 blocks, they can increase 1/2 + 1/4 + 1/6 + 1/8 + 1/10 + 1/12 + 1/14 + 1/16 + 1/18 + 1/20which increases up to about 1.464 block length beyond the edge. But what is the limit of how far we can do blocks? For that, we must add most of the many lower terms. The resulting pattern brings an impressive resemblance to one of the most famous endless amount In mathematics, the harmonic series, taken the reciprocation of each counting number (that is, 1 divided by every positive integer) and supports them all:
1 + 1/2 + 1/3 + 1/4 + 1/5 + … and so forever.
If you look so closely, you may notice that overhangs from block-sweating trouble is exactly half of each of these terms: 1/2 + 1/4 + 1/6 + 1/8 + 1/10 + …
AldanabotThe mathematical branch that dug into how the change, taught us even when increasing the amounts of value and sometimes it drives forever. The general of the harmonic series is less slow. The first 100,000 terms increased up to 12.1 while the first million terms were equal to about 14.4. However, in a step-by-step SNA, the Harmonic Series continues forever.
Each individual overhangs block-sweating problem is equal to half a term of harmonic series. Because half end is still infinite, the potential overhang of the tower does not bound.
Of course, the interpretation of pure maths often comes with hurdles, but the problem with the block offers a fun decree of dexterity. With only four blocks, you need to expand the top of a total block length past the edge (1/2 + 1/4 + 1/6 + 1/8 = ~ 1.042). In order to fulfill my journalistic hard work, I tried it at home with cards playing my coffee table. After a few minutes of patient tinkering, I managed to balance the top card more than the edge, hanging across the table, and as I was a magician.
Two full lengths of block above any surface require 31 pieces. While million pieces also don’t get a full 10 block length because the value of the first 100 million Harmonic Series terms divided by about 9.5. So take a grit to reach the Grand Canyon. In many scales, physics began to enjoy mathematicians. But in the ideal conditions in which the mass center and the harmonic series only rule the Roost, the possibilities literally endless.










